Capítulo 3 Teste de hipótese

Os pesquisadores às vezes estão interessados em verificar as diferenças variáveis ou entre grupos de pessoas. […] Por exemplo, se tomarmos dois grupos de pessoas e aleatoriamente designarmos um grupo a um programa de pílulas dietéticas e o outro grupo a um programa de pílulas de açúcar (que eles acham que irá auxiliá-los na perda de peso), se as pessoas que tomam as pílulas dietéticas perderem mais peso do que as que tomam pílulas de açúcar podemos inferir que as pílulas dietéticas causaram a perda de peso. (Field, Miles, and Field 2012). Diante disso, por meio de testes estatísticos pode constatar se a média de perde de peso em entre as pessoas que tomaram a pílula dietática é maior do que as pessoas que tomaram a pílula de açúcar.

Para tomar a decisão sobre qual teste estatístico utilizar, é importante observar o receituária de análise bivariada apresentado na figura abaixo. Está fora do escopo desse tutorial abordar todos os testes mencionados no receituário. Apenas alguns deles serão trabalhados nesse tutorial. No entanto, a regra para decisão está principalmente ancorada na análise dos tipos de variáveis avaliadas. Se temos duas variáveis categóricas sendo análisadas, devemos usar o teste qui-quadrado. Se temos uma variável categórica (com 2 categorias apenas) e uma variável contínua, é sugerido usar o test t de Student. Ao passo que, se temos uma variável categórica (com mais de 2 categorias apenas) e uma variável contínua, é sugerido usar o teste da análise de variância (ANOVA). E assim por diante de acordo com as indicações do receituário.

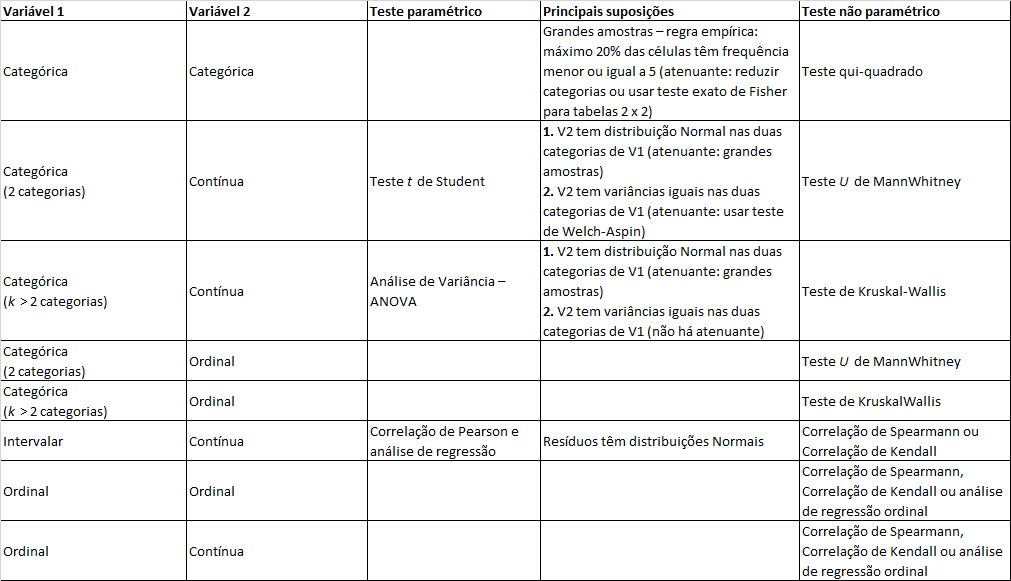
Em relação à decisão por teste paramétrico ou não paramétrico, a decisão é tomada diante do aderência às suposições do teste paramétrico a ser utilizado. Quando as suposições são atendidas, é indicado utilizar o teste paramétrico pertinente. Quando elas não são atendidas, é indicado utilizar o teste não paramétrico pertinente.

Testes paramétricos são aqueles que fazem suposições sobre os parâmetros da distribuição da população da qual a amostra é extraída. Geralmente a suposição é de que os dados populacionais são normalmente distribuídos. Os testes mais populares para checar se os dados seguem uma distribuição normal são: teste de Kolmogorov-Smirnov, teste de Anderson-Darling e teste de Shapiro-Wilk. Por fim, os testes não paramétricos são “livres de distribuição” e, como tal, podem ser usados para variáveis não normais.

3.1 Análise do teste de hipótese

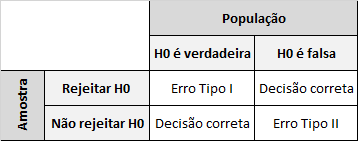
Em todo teste de hipótese, os resultados permitem que o pesquisador tome a decisão rejeitar ou não rejeitar uma hipótese estatística através da evidencia fornecida pela amostra. A figura a seguir resume a decisão genérica envolvida em qualquer teste de hipótese. H0 é a hipótese nula do teste realizado.

Os erros tipo I e tipo II são os erros possíveis ao realizarmos um teste de hipótese:

• O erro tipo I pode ocorrer se os resultados a partir da amostra obtida levarem o pesquisador a rejeitar a hipótese nula (H0), quando na realidade ela é verdadeira.
• erro tipo II pode ocorrer se os resultados a partir da amostra obtida levarem o pesquisador a não rejeitar a hipótese nula e na verdade ela é falsa.

A seguir, visando avaliar na prática como ocorre a tomada de decisão em um teste de hipótese, avaliaremos a aplicação do teste t de Student.

3.2 Teste t de Student

Conforme a figura do receituário de análise bivariada apresentado acima, o teste t de Student é o teste indicado quando analisamos uma variável categórica (com 2 categorias) e uma variável contínua. A figura a seguir resume esse proceso de tomada de decisão:

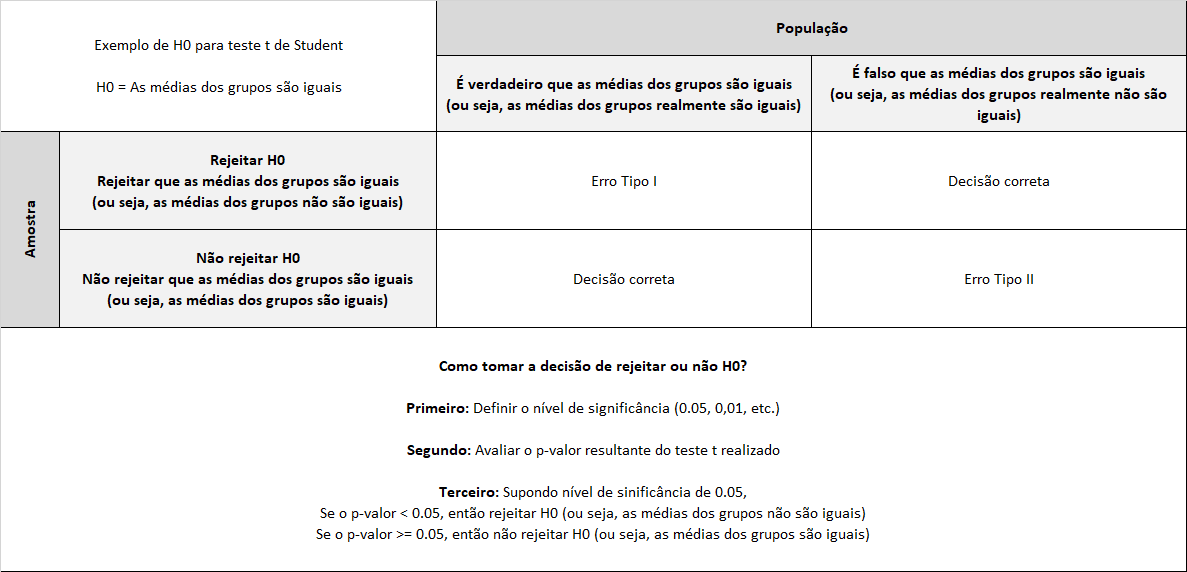
3.2.1 Teste t de Student para amostras dependentes (repeated measures ou paired samples)

O teste t de Student para amostras dependentes (repeated measures ou paired samples) é usado para comparar as médias amostrais de dois grupos relacionados. Isso quer dizer que as mensurações realizadas para os dois grupos comparados vêm das mesmas pessoas. O objetivo deste teste é determinar se há uma mudança de uma medição para outra mantendo as mesma pessoas analisadas, porém mudando as condições nas quais as mensurações são realizadas.

A seguir temos a aplicação do teste t de Student para amostras dependentes no software R. Vamos utilizar a base de dados SpiderLong.dat disponibilizada por (Field, Miles, and Field 2012) no repositório digital de seu livro. Para fins da aplicação do teste t de Student para amostras dependentes, vamos assumir que essa base dados vem de um estudo realizado com uma amostra de 12 pessoas para avaliar o seu nível de ansiedade ao visualizarem aranhas. O experimento buscou medir o nível de ansiedade gerado quando as pessoas viam fotografias de aranhas e quando essas mesmas pessoas viam aranhas reais.

# Carregar base de dados SpiderLong.dat do livro de Field et al. (2012)

SpiderLong <- read.delim(
  # No parâmetro file, use o caminho para a pasta onde está 
  # o arquivo SpiderLong.dat em seu computador.
  file = "dados/SpiderLong.dat",  
  header = TRUE
  )  

# A título de investigação, vamos calcular as médias parta a variável ansiedade 
# para os dois grupos testados: aranhas em fotografias e aranhas reais 

SpiderLong %>% 
  group_by(Group) %>% 
  summarise(
    Anxiety_Media = mean(Anxiety)
  )

## # A tibble: 2 × 2
##   Group       Anxiety_Media
##   <chr>               <dbl>
## 1 Picture                40
## 2 Real Spider            47

Calculando a média de cada grupo, percebemos que o nível de ansiedade gerado quando as pessoas viram uma aranha real foi, em média, 7 pontos maior do que quando viram fotografias de aranhas. A pergunta que fica é: essa diferença é estatisticamente significante (considerando-se um nível de significância de 0.05)?

Para responder essa pergunta, precisamos realizar um teste t de Student para amostra dependentes conforme é realizado no código abaixo.

# Ajustar a base de dados para estimar teste t para amostras dependentes (repeated measures)

PictureCol <- SpiderLong %>% 
  filter(Group == "Picture") %>% 
  pull(Anxiety)

RealSpiderCol <- SpiderLong %>% 
  filter(Group == "Real Spider") %>% 
  pull(Anxiety)


# Realizar o teste para amostras dependentes (repeated measures)

t.test(
  x = PictureCol,
  y = RealSpiderCol,
  paired = TRUE
  )

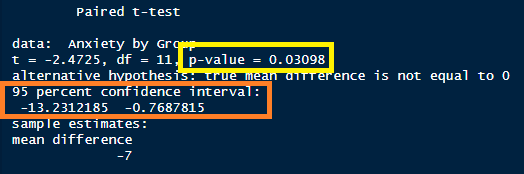
Diante dos resultados acima, devemos avaliar principalmente o resultado apresentado para o “p-value” (resultado grifado em amarelo na figura acima). Se p-value fosse maior ou igual a 0.05, então não poderíamos rejeitar a hipótese nula (H0) de que as médias dos grupos são iguais. No entanto, como resultado obtido para o p-value é 0,03098, portanto, menor do que 0,05, podemos rejeitar a hipótese nula H0.

Assim, podemos afirmar, considerando um nível de significância de 0,05, que as médias dos grupos não são iguais. Ou seja, diante do experimento realizado concluímos que visualizar uma aranha real gera mais ansiedade do que visualizar fotografias de aranhas.

Além desse resultado, o output do test t de Student para amostras dependentes também nos retorna o intervalo de confiança para a diferença entre as médias dos dois grupos. Sabemos que a diferença de médias encontrada na amostra foi de 7 pontos. No entanto, diante do resultado obtido, podemos inferir que essa diferença de média, com nivel de confiança de 95%, estará dentro de um intervalo de $[13,23 ; 0,77] .

3.2.2 Teste t de Student para amostras independentes

O teste t de amostras independentes é usado para comparar médias amostrais de dois grupos não relacionados. Isso quer dizer que as mensurações realizadas para os dois grupos comparados vêm de pessoas diferentes. O objetivo deste teste é evidenciar se as amostras são diferentes umas das outras.

A seguir temos a aplicação do teste t de Student para amostras independentes no software R. Vamos utilizar a base de dados SpiderLong.dat disponibilizada por (Field, Miles, and Field 2012) no repositório digital de seu livro. Para fins da aplicação do teste t de Student para amostras independentes, vamos assumir agora que essa base dados vem de um estudo realizado com uma amostra de 24 pessoas para avaliar o seu nível de ansiedade ao visualizarem aranhas. O experimento buscou medir o nível de ansiedade gerado quando 12 dessas pessoas viram fotografias de aranhas e quando as outras 12 pessoas viram aranhas reais.

# A título de investigação, vamos calcular novamente as médias para a variável 
# ansiedade para os dois grupos testados: aranhas em fotografias e aranhas reais 

SpiderLong %>% 
  group_by(Group) %>% 
  summarise(
    Anxiety_Media = mean(Anxiety)
  )

## # A tibble: 2 × 2
##   Group       Anxiety_Media
##   <chr>               <dbl>
## 1 Picture                40
## 2 Real Spider            47

Novamente, é claro, calculando a média de cada grupo, percebemos que o nível de ansiedade gerado quando as pessoas viram uma aranha real foi, em média, 7 pontos maior do que quando viram fotografias de aranhas. Agora, porém essa diferença foi obtido considerando que temos pessoas diferentes nos dois grupos. A pergunta que fica é: essa diferença é estatisticamente significante (considerando-se um nível de significância de 0.05)?

Para responder essa pergunta, precisamos realizar um teste t de Student para amostra independentes conforme é realizado no código abaixo.

yuen(

formula = Anxiety ~ Group,

data = SpiderLong,

tr = .2,

alpha = .05

)

# Realizar o teste para amostras independentes

t.test(
  formula = Anxiety ~ Group, 
  data = SpiderLong, 
  paired = FALSE
  )

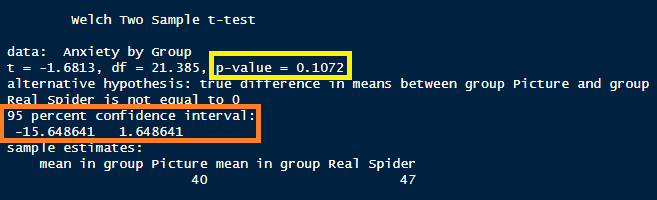
Diante dos resultados acima, devemos avaliar principalmente o resultado apresentado para o “p-value” (resultado grifado em amarelo na figura acima). Sabemos que quando o p-value é maior ou igual a 0.05 não podemos rejeitar a hipótese nula (H0) de que as médias dos grupos são iguais. Diante disso, dado que o resultado obtido para o p-value é 0,1072, concluímos que não rejeitar a hipótese nula H0.

Assim, não podemos afirmar, considerando um nível de significância de 0,05, que as médias dos grupos não são iguais. Ou seja, diante do experimento realizado com uma amostra de 24 pessoas (separadas em dois grupos distintos de 12 pessoas), não podemos concluir que visualizar uma aranha real gera mais ansiedade do que visualizar fotografias de aranhas.

Além desse resultado, o output do test t de Student para amostras independentes também nos retorna o intervalo de confiança para a diferença entre as médias dos dois grupos. Sabemos que a diferença de médias encontrada na amostra foi de 7 pontos. No entanto, diante do resultado obtido, podemos inferir que essa diferença de média, com nivel de confiança de 95%, estará dentro de um intervalo de $[15,65 ; -1,65] . Como nosso intervalo de confiança cruza o 0 (zero), temos a comprovação da não significância estatística da diferença de médias testada.

3.3 Análise de variância (ANOVA) para amostras independentes

Conforme a figura do receituário de análise bivariada apresentado acima, o teste t de Student é o teste indicado quando analisamos uma variável categórica (com mais do que 2 categorias) e uma variável contínua. É o caso no qual temos mais de dois grupos para comparar, para uma determinada métrica continua, se pelo menos uma das médias dos grupos difere das demais. A figura a seguir resume esse proceso de tomada de decisão:

A seguir temos a aplicação da ANOVA no software R. Vamos utilizar a base de dados Viagra.dat disponibilizada por (Field, Miles, and Field 2012) no repositório digital de seu livro. Essa base dados vem de um estudo realizado com uma amostra de 15 pessoas para avaliar o seu nível de libido ao tomarem diferentes doses do medicamento viagra (placebo (1), low dose (2) e high dose (3)).

# Carregar base de dados Viagra.dat do livro de Field et al. (2012)

Viagra <- read.delim(
  # No parâmetro file, use o caminho para a pasta onde está 
  # o arquivo Viagra.dat em seu computador.
  file = "dados/Viagra.dat",  
  header = TRUE
  ) %>% 
  mutate(
    dose = as.factor(dose)
  )

# A título de investigação, vamos calcular as médias parta a variável libido 
# para os três grupos testados: Placebo (1), Low dose (2) e High Dose(3) 

Viagra %>% 
  group_by(dose) %>% 
  summarise(
    libido_Media = mean(libido)
  )

## # A tibble: 3 × 2
##   dose  libido_Media
##   <fct>        <dbl>
## 1 1              2.2
## 2 2              3.2
## 3 3              5

Calculando a média de cada grupo, percebemos que o nível de libido gerado varia quando as pessoas tomam placebo (2,2), low dose (3,2) ou high dose (5,0). A pergunta que fica é: alguma dessas diferenças são estatisticamente significantes (considerando-se um nível de significância de 0.05)?

Para responder essa pergunta, precisamos realizar uma ANOVA.

No entanto, antes de realizar a ANOVA, precisamos primeiro garantir que uma importante suposição do modelo satisfeita, a de que há homogeneidade entre as variâncias dos grupos comparados. Para isso, podemos utilizar o teste de Levene.No teste de Levene a hipótese nula (H0) é de que as variâncias são homogêneas entre os grupos. Portanto, para que a suposição homogeneidade entre as variâncias dos grupos comparados seja confirmada, não podemos rejeitar H0 no teste de Levene.Ou seja, o p-value deve ter valor maior ou igual a 0,05.

Para performar o teste de Levene basta executar o seguinte código no software R:

# Executar o teste de Levene para checar se suposição de homogeneidade 
# entre as variâncias dos grupos comparados é atendida
# Para executar a funcao leveneTest é preciso carregar o pacote "car"

leveneTest(
  y = libido ~ dose, 
  data = Viagra
  )

## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  2  0.1176   0.89
##       12

O valor do p-value da estatística F do Levene de Levene é bastante não significante (p-value = 0,89). Como o p-value é maior do que 0,05, isso significa que para esses dados as variâncias entre os grupos analisados são muito semelhantes. Caso o teste de Levene rejeitasse a hipótese nula (H0), tendo um p-value menor do que 0,05, então a indicação seria para o pesquisador utilizar o teste não paramétrico Kruskal-Wallis.

Uma vez validada a suposição de homogeneidade entre as variâncias dos grupos comparados, podemos ir adiante e performar a ANOVA utilizando o código a seguir:

# Executar a análise ANOVA

viagraAnova <- aov(
  formula = libido ~ dose, 
  data = Viagra
  )

# Solicitar o resumo dos resultados para a ANOVA

summary(viagraAnova)

##             Df Sum Sq Mean Sq F value Pr(>F)  
## dose         2  20.13  10.067   5.119 0.0247 *
## Residuals   12  23.60   1.967                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Diante dos resultados acima, devemos avaliar principalmente o resultado apresentado para o “p-value” (resultado grifado em amarelo na figura acima). Sabemos que quando o p-value é maior ou igual a 0.05 não podemos rejeitar a hipótese nula (H0) de que as médias de todos os grupos são iguais. No entanto, como resultado obtido para o p-value é 0,0247, portanto, menor do que 0,05, podemos rejeitar a hipótese nula H0.

Assim, podemos afirmar, considerando um nível de significância de 0,05, que as médias de todos os grupos não são iguais. Ou seja, diante do experimento realizado concluímos que o tamanho da dose do medicamento gera nivel de libido diferente em pelo menos um dos pares possíveis de combinações entre os grupos analisados.

Agora já sabemos pelo menos um dos pares possíveis de combinações entre os grupos analisados possuem diferença de médias estatisticamente significantes. A pergunta final é: quais desses pares de possíveis possuem diferença de médias estatisticamente significantes?

Para responder essa pergunta precisamos proceder com um teste post-hoc: o teste Tukey Honest Significant Differences (Tukey HSD). Para executá-lo, basta usar o seguinte código no software R:

# Executar o teste Tukey Honest Significant Differences (Tukey HSD)

TukeyHSD(viagraAnova)

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = libido ~ dose, data = Viagra)
## 
## $dose
##     diff        lwr      upr     p adj
## 2-1  1.0 -1.3662412 3.366241 0.5162761
## 3-1  2.8  0.4337588 5.166241 0.0209244
## 3-2  1.8 -0.5662412 4.166241 0.1474576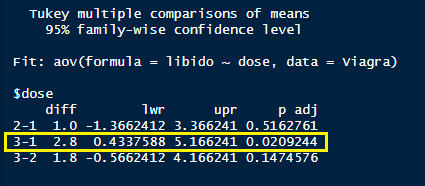

Diante dos resultados acima, devemos avaliar principalmente o resultado apresentado para a coluna “p-adj”. Nas linhas nas quais o valor do p-adj for menor do que 0,05, tem uma diferença de média estatisticamente significante. Cada linha representa um par avaliado dos pares possíveis entre os grupos avaliados (Placebo (1), Low dose (2) e High dose(3)).

• Na primeira linha, é avaliada a diferença de médias entre Placebo (1), Low dose (2): p-adj = 0.5163. Conclusão: Não é possível rejeitar a hipótese nula (H0) de que as médias são iguais. Ou seja, Não há diferença de médias estatisticamente significante entre esses grupos.
• Na segunda linha, é avaliada a diferença de médias entre Placebo (1) e High dose(3): p-adj = 0.0209. Conclusão: É possível rejeitar a hipótese nula (H0) de que as médias são iguais. Ou seja, Há diferença de médias estatisticamente significante entre esses grupos. Essa é a linha grifada em amarelo na figura acima.
• Na terceira linha, é avaliada a diferença de médias entre Low dose (2) e High dose(3): p-adj = 0.1475. Conclusão: Não é possível rejeitar a hipótese nula (H0) de que as médias são iguais. Ou seja, Não há diferença de médias estatisticamente significante entre esses grupos.

3.4 Teste qui-quadrado para amostras independentes

Às vezes, não estamos interessados em medidas contínuas, mas em variáveis categóricas (Field, Miles, and Field 2012). Ou seja, ao invés de testar a diferença de médias de uma variável contínua entre dois ou mais grupos (uma variável contínua e uma variável categórica), podemos querer analisar duas variáveis categóricas. Nesses casos, não devemos calcular a média de uma variável categórica, pois não muito sentido seu resultado. Diante disso, para proceder tal análise, precisamos avaliar as frequências observadas para os grupos formados pelo cruzamento entre essas duas variáveis categóricas. Imagine que você está realizando um experimento de campo no qual objetiva testar se uma promoção de vendas direcionada para clientes em risco de deserção (abandonaram a empresa). Seu desejo é observar o impacto de realizar ou não a promoção de vendas versus a decisão de um cliente desertar ou não. Temos portanto duas variáveis categóricas: (\(i\)) Promoção de vendas (realizar a promoção ou não realizar promoção alguma) e (\(ii\)) Deserção (cliente desertou ou não). Avaliar se as fraquências diferem entre os quatro grupos formados pelo cruzamento dessas duas variáveis é um típico problema a ser resolvido utilizando o teste qui-quadrado.

O uso to teste qui-quadrado, mesmo sendo um teste não-paramétrico, possui algumas suposição para que possa ser utilizado:

• A amostras devem ser independentes, ou seja, cada indivíduo é alocado para apenas um grupo entre os grupos formados pelo cruzamentos entre as variáveis categóricas.
• Cada grupo formados pelo cruzamentos entre as variáveis categóricas deve ter frequência maior ou igual a 5.

Para fins de aplicação prática do teste qui-quadrado, vamos aplicar o exemplo hipótético trazido por (Field, Miles, and Field 2012). Imagine que queremos testar qual recompensa impacta mais a chance sucesso ao ensinar gatos a dançar. Para esse exerimentos, escolheu-se 200 gatos e tentou-se treiná-los, durante uma semana, para dançar dando-lhes comida ou carinho como recompensa pelo comportamento de dança. No final da semana ele contou quantos animais podiam dançar e quantos não podiam. Há duas variáveis categóricas aqui: tipo de recompensa no treinamento (o animal foi treinado usando comida ou carinho, não ambos) e dança (o animal aprendeu a dançar ou não). Ao combinar categorias, acabamos com quatro categorias diferentes. Precisamos, então, contar quantos gatos se enquadram em cada categoria.

Com o objetivo de aplicar o teste qui-quadrado nesse exemplo, vamos utilizar a base de dados cats.dat disponibilizada por (Field, Miles, and Field 2012) no repositório digital de seu livro.

# Carregar base de dados cats.dat do livro de Field et al. (2012)

Cats <- read.delim(
  # No parâmetro file, use o caminho para a pasta onde está 
  # o arquivo Viagra.dat em seu computador.
  file = "dados/cats.dat",  
  header = TRUE
  ) 

# Calcular a tabela de contingência entre as duas variáveis
Cats %>% 
  select(Training, Dance) %>% 
  table()

##                      Dance
## Training               No Yes
##   Affection as Reward 114  48
##   Food as Reward       10  28

# Realizar o teste qui-quadrado não usando a correção de Yates - Recomendado
chisq.test(
  x = Cats$Training,
  y = Cats$Dance,
  correct = FALSE 
  )

## 
##  Pearson's Chi-squared test
## 
## data:  Cats$Training and Cats$Dance
## X-squared = 25.356, df = 1, p-value = 4.767e-07

O teste acima calcula qui-quadrado padrão. Já o teste calculado no código abaixo, utiliza a correção de Yates. Essa é uma correção que visa mitigar a chance de incorrer em um erro tipo I, que pode ocorrer quando temos o qui-quadrado aplicado para duas variáveis categóricas com duas categorias cada. No entanto, conforme (Field, Miles, and Field 2012), recomenda-se utilizar o teste qui-quadrado padrão.

# Realizar o teste qui-quadrado usando a correção de Yates
chisq.test(
  x = Cats$Training,
  y = Cats$Dance,
  correct = TRUE 
  )

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  Cats$Training and Cats$Dance
## X-squared = 23.52, df = 1, p-value = 1.236e-06

A estatística qui-quadrado testa se as duas variáveis são independentes. Se o p-value for pequeno o suficiente (menor que 0.05), rejeitamos a hipótese nula de que as variáveis são independentes e ganhamos confiança na hipótese alternativa de que eles estão de alguma forma relacionados (Field, Miles, and Field 2012).
O resultado altamente significativo (p-value = 4.767e-07) indica que existe uma associação entre o tipo de recompensa no treinamento e se o gato dançou ou não. O que queremos dizer com associação é que o padrão de respostas (ou seja, a proporção de gatos que dançaram para a proporção que não o fez) nas duas condições de treinamento é significativamente diferente. Esta descoberta reflete o fato de que quando a comida é utilizada como recompensa, cerca de 74% dos gatos aprendem a dançar e 26% não, ao passo que quando se usa o carinho, ocorre o contrário (cerca de 70% se recusam a dançar e 30% dançam). Portanto, podemos concluir que o tipo de treinamento utilizado influencia significativamente os gatos: eles vão dançar por comida, mas não por carinho!

3.5 Correlação de Pearson (bivariada)

Quando desejamos testar a associação entre duas variáveis contínuas, o teste adequado é a correlação de Pearson. A correlçao de Pearson testa a o nível a direção da associação entre a variabilidade de uma variável A e a variabilidade de uma variável B. O coeficente de correlçao de Pearson varia de -1 até 1. Quanto maior e mais positiva for a asssociação entre as variabilidades das duas variáveis, mais próximo de 1 será o valor resultante. Quanto maior e mais negativa (inversa) for a asssociação entre as variabilidades das duas variáveis, mais próximo de -1 será o valor resultante. Qquando mais fraca for a asssociação entre as variabilidades das duas variáveis, mais próximo de 0 será o valor resultante. O teste da correlação de Pearson é realizado conforme o código abaixo no software R. Para isso, vamos usar a base de dados Exam Anxiety.dat disponibilizada por (Field, Miles, and Field 2012) no repositório digital de seu livro. Essa base de dados é referente a um estudo no qual um psicólogo desejava avaliar os efeitos do estresse/ansiedade pré-prova de estudantes nos seus respectivos desempenhos na prova. A ansiedade foi medida antes da prova usando um instrumento de medição que possui nota máxima igual a 100.

# Carregar base de dados Exam Anxiety.dat do livro de Field et al. (2012)

ExamAnsiety <- read.delim(
  # No parâmetro file, use o caminho para a pasta onde está 
  # o arquivo Viagra.dat em seu computador.
  file = "dados/Exam Anxiety.dat",  
  header = TRUE
  ) 

# Calcular a correlçao de Pearson entre as variáveis Exam (nota na prova) e Ansiety

cor.test(
  y = ExamAnsiety$Exam, 
  x = ExamAnsiety$Anxiety  
  )

## 
##  Pearson's product-moment correlation
## 
## data:  ExamAnsiety$Anxiety and ExamAnsiety$Exam
## t = -4.938, df = 101, p-value = 3.128e-06
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.5846244 -0.2705591
## sample estimates:
##        cor 
## -0.4409934

O resultado indica que a correlação de Pearson entre o desempenho na prova e o nível de ansiedade pré-prova foi de -0,441. Ou seja, quanto maior a ansiedade temos uma tendência de ter um nota menor, embora o coeficiente de correlação seja apenas moderado, não é alto (próximo de -1). O teste de correlação também nos diz que o resultado a hipótese nula de que a correlçao é igual a 0 foi rejeitada, com pvalue = 3.128e-06. Além disso, o intervalo de confiança de 95% variou de –0.585 a –0.271, o que não cruza zero. Isso nos diz que podmeos inferir que na população o valor real da correlação é negativo entre ansiedade pré-prova e nota da prova

References

Field, Andy P., Jeremy Miles, and Zoë Field. 2012. Discovering Statistics Using R. London ; Thousand Oaks, Calif: Sage.